Messverfahren

Die hier relevanten Quellen für ionisierende Strahlung sind radioaktive Substanzen, d.h. Stoffe, die spontanen Umwandlungsprozessen unterliegen. Dies geschieht u.a. bei Isotopen, deren Atomkerne im Gegensatz zu ihren üblichen stabilen Varianten instabil sind. Ihre Atomkerne spalten sich spontan in leichtere (oft auch wieder instabile) Kerne, und sie setzen dabei Teilchen (Heliumkerne oder Elektronen, Alpha- bzw. Betastrahlung) und/oder Energie (hochenergetische Quanten, Gamma-Strahlung) frei.

Strahlungsdetektoren

Detektieren kann man diese Strahlung, indem man ihre ionisierende Wirkung technisch nutzt. Der klassische Detektor ist das Geiger-Müller-Zählrohr: Ein gasdichter Zylinder ist an seiner Innenseite mit einer elektrisch leitenden Schicht ausgekleidet. Isoliert davon befindet sich in seiner Mittelachse eine dünner Draht. Der Zylinder ist mit einem Edelgas (z.B Argon oder Xenon) gefüllt. Ein Teilchen oder ein Quant, das den Zylinder durchtritt und dabei ein Gasatom trifft, ionisiert dieses. D.h. es spaltet das Gasatom in ein positiv geladenes Ion und ein (negativ geladenes) Elektron auf. Wird zwischen die Elektroden – dem leitenden Mantel und dem Draht in der Mitte – eine Spannung (von z.B. 500 V) angelegt, bewegen sich die frei gewordenen Elektronen zur positiven Elektrode, die ionisierten Atome zur negativen Elektrode, wo sie mit einem Elektron rekombinieren. Die Folge ist ein elementarer Stromimpuls für jede Interaktion der Gasfüllung.

Andere Detektorverfahren nutzen Ionisierungprozesse in Halbleiterschichten oder sie verwenden Szintilatoren, in denen energiereiche Quanten  Photonenlawinen auslösen, die mit optischen Detektoren (z.B. Photodioden) in elektrische Impulse umgesetzt werden.

Messtechnische Umsetzung

Die Anzahl pro Zeiteinheit der Ereignisse, die zu elektrischen Impulsen führen, ist ein Maß für die Ortsdosisleistung. Um diese anzuzeigen, werden die Impulse über ein Zeitinterval gezählt (Geräte für diesen Zweck werden deshalb auch als 'Geiger-Zähler' bezeichnet). Da der Erzeugung der Impulse ein Zufallsprozess zugrunde liegt, hängt die Wahl des Zeitintervals entscheidend davon ab, welche Ziele mit einer Messung verfolgt werden.

Strahlungsmesswerte sind stochastische Größen

Das Auftreten eines Impulses ist ein Zufallsereignis, das von mehreren Prozessen abhängt. Schon die spontane Spaltung ('Zerfall') eines Atoms des radioaktiven Isotops gehorcht einem Zufallsprozess. Da das bei der Spaltung frei werdende Teilchen oder Quant in jede beliebige Raumrichtung abgestrahlt werden kann, hängt es vom Zufall ab, ob es auf den Detektionsraum des Detektors trifft. In diesem hängt es wieder vom Zufall ab, ob eine Interaktion stattfindet, die zu einem Ladungsimpuls führt. Alle diese Wahrscheinlichkeiten multiplizieren sich und führen zu streuenden Ergebnissen einer Impulszählung über ein festgelegtes Zeitintervall.

Die Streuung der Zählergebnisse wird durch eine Wahrscheinlichkeitsdichtefunktion beschrieben. Sie hat die Form der bekannten gaußschen Glockenkurve (korrekt gehorcht der Zufallsprozess einer Poisson-Verteilung, die jedoch durch eine Gauß-Verteilung gut angenähert werden kann). Die Lage des Maximums der Kurve gibt den Mittelwert einer großen Zahl von Zählergebnisse wieder. Die Flächen unter der Kurve geben an, wie hoch der Anteil der Zählergebnisse erwartet werden kann, die in das jeweiligen Segment fallen.

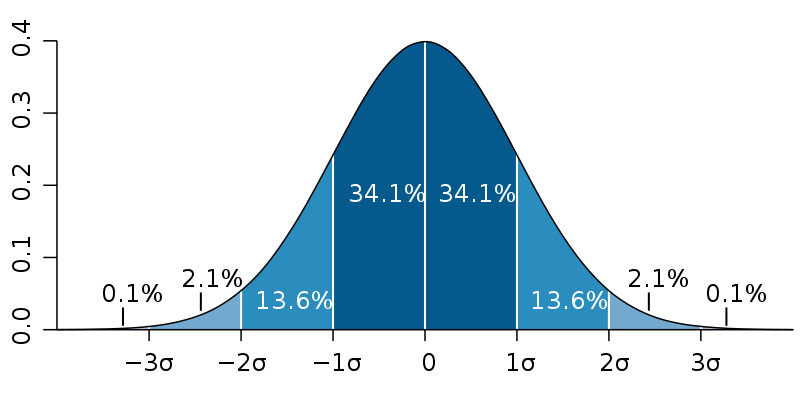Wahrscheinlichkeitsdichtefunktion (Urheber: M.W.Toews, Quelle: Wikipedia)

Charaterisiert wird die Gauß-Kurve durch die Lage des Mittelwertes (auch 'Erwartungswert' genannt) und die Standardabweichung σ, hier die Breite der Segmente. Bei einer Poisson-Verteilung ergibt sich die Standardabweichung aus der Quadratwurzel des Erwartungswertes. Ein Zahlenbeispiel:

• Im Mittel sei die Zahl der in einem Zeitinterval von 15 Minuten gezählten Ereignisse 100 (dies entspricht etwa den derzeitigen TDRM-Sensorstationen).
• Die Standardabweichung σ wäre in diesem Fall 10, d.h. 10% des Mittelwertes.
• Es  fielen damit ca. 2/3 aller Zählergebnisse in das Intervall 90 bis 110, 1/3 der Ergebnisse lägen noch außerhalb eines Variationsbereiches von ±10%.
• Um diesen Variationsbereich auf ±1% zu reduzieren, müsste das Zählintervall auf 25 Stunden ausgedehnt werden. 
• Andererseits schrumpft der Variationsbereich auch bei einer Erhöhung Strahlungsleistung. Er betrüge bei einem außergewöhlichen Anstrieg auf beispielsweise die 10fache Dosisleistung nur noch ca. ±3% relativ zum aktuellen Messwert.

Das Zahlenbeispiel verdeutlicht, dass bei der Messung einer stochastischen Größe ein Kompromiss zwischen Sensibilität und Ansprechzeit gewählt werden muss.

Wir haben uns mit der Wahl eines Zählintervalls von 15 Minuten zugunsten einer kurzen Ansprechzeit entschieden, denn uns erscheint es wichtig, dass wir massive Unregelmäßgkeiten möglichst unverzüglich darstellen können. Unsere Sensorstationen liefern jede Minute das Ergebnis einer Zählung über die jeweils zurückliegenden 15 Minuten ('sliding window'), so dass grobe Trendänderungen bereits nach wenigen Minuten bemerkbar werden.

Zeitdiagramm der Untergrundstrahlung: Die Variation der Messwerte ist stochastischen Ursprungs und nicht durch Fluktuationen der Dosisleisung in der umgebenden Atmosphäre bedingt